Jamovi教程的第三部分主要介绍了分析数据的几种方式。

最基础的方法是使用 descriptive statistics (统计数据分析) 功能进行分析。其次Jamovi还提供了多种图表分析的功能，包括：

Histograms （直方图）

Density plots （密度图）

Box plots （箱形图）

Violin plots （小提琴图）

Dot plots （点状图）

Bar plots （条形图）

其实在介绍Jamovi的第一篇更新里，我们已经介绍了这其中的一部分图表，今天我们详细地看一下每一种图表的使用方法。

往期更新请参考：Jamovi 01- Getting started part 1

1. Descriptive statistics

首先选择 Open - data library - Bugs（Ryan, Wilde & Crist, 2013）

Bugs 这个数据的来源会放在更新的最后，感兴趣的可以看一下。简单来说，研究者通过事前实验选出了8种让人觉得害怕和恶心的昆虫，被试者需要看这几种昆虫的图片来说明自己害怕和恶心的心情。其中害怕 (Frightening)标记为F, 恶心 (Disgusting)标记为D。而使人害怕和恶心的程度有L (Low) 和 H (High)之分，这样就有了 LDLF, LDHF, HDLF, HDHF 四个大类。

除此之外，Bugs还给出了被试者的性别，地区和受教育程度这三项信息。

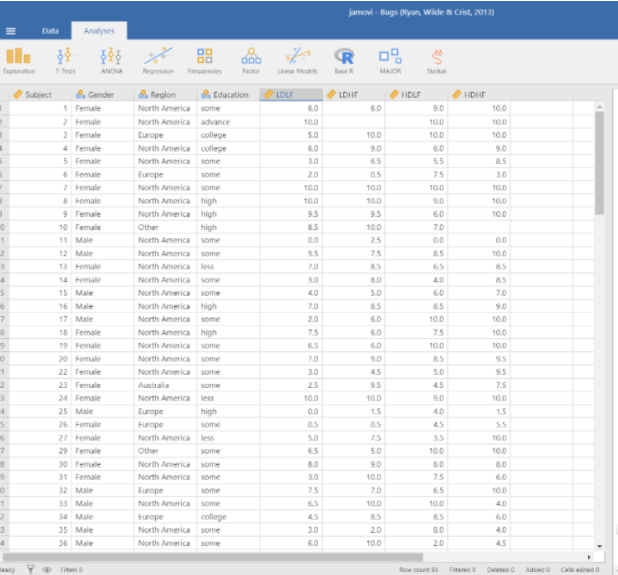
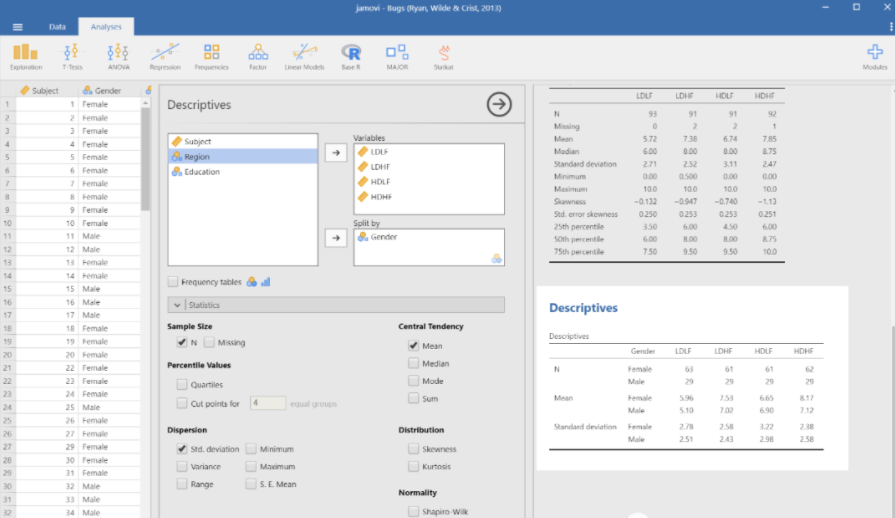
选择左上角的 Exploration - Descriptives 我们就能看到新的窗口。

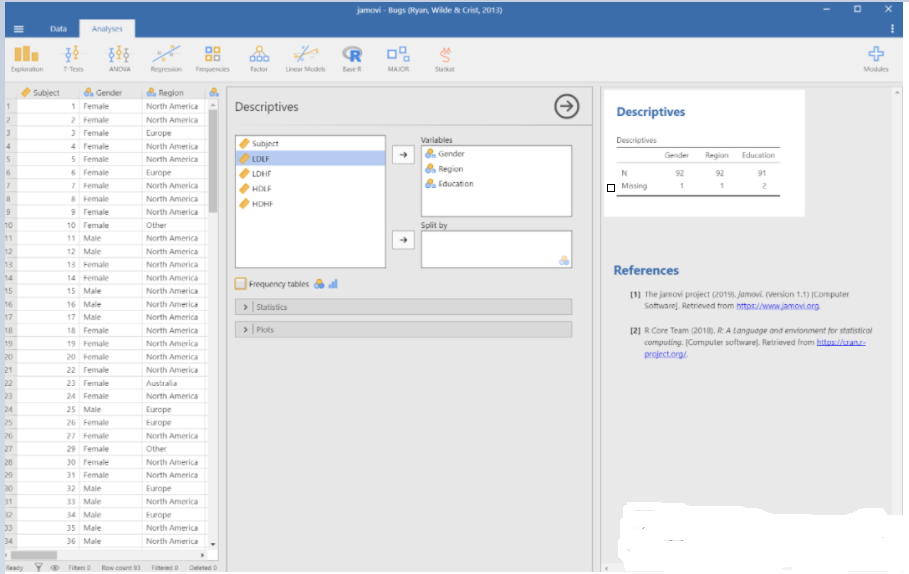
先来看预测变量 (predictor variables)的数据分析。预测变量指的是，通过这个变量我们可以预测相应的结果。在这里，指的就是gender，region 和 education这三项。因为这三个变量都是定类变量 (nominal variable)/分类变量 (categorical variable)，所以不需要知道它们的均值，中位值和标准偏差，这些值是在有定量变量 (quantitative variable) 或者连续变量 (continuous variable)时才需要具体关注的。因此简单地选择Statistics 下面的 N(number) 和 Missing就能直观地看到我们所有的案例数。对于定类变量来说，了解它们的频率 (frequency)还是很有意义的，所以再选择频率，得到下面的结果。

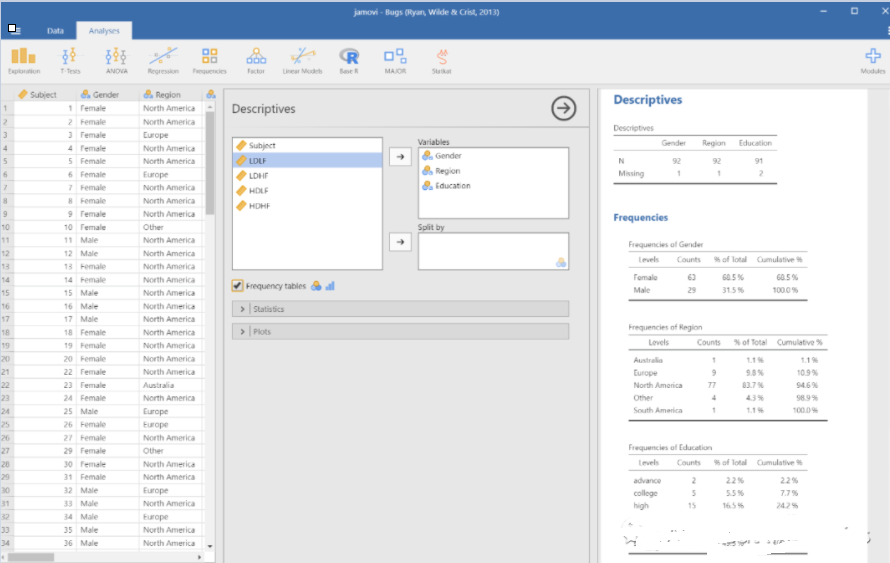
频率表详细地给出了各个类别里的案例的值及其在所有案例中占据的比例。比如，被试者中有约68.5%是女性，31.5%是男性。从地区来看，大部分被试者来自于北美，10%的被试者来自欧洲。从受教育程度程度来看，大约有16.5%的人是高中学历。

再来看结局变量 (outcome variables)。在这里，结局变量就是LDLF, LDHF, HDLF, HDHF这四项了。这四类值是实验中，给被试者0-10的评定量表，让被试者自我评定后得出的结果。因为这四类值是定量结果 (quantitative outcomes)，所以默认的均值，中位值都能在结果里看到。

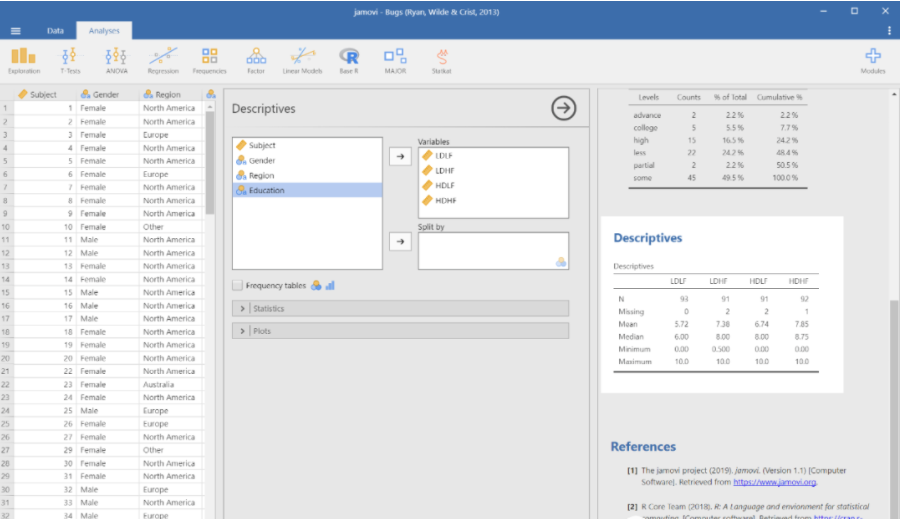
但这并不是全部，在 Statistics下面，选择 Std. Deviation (标准偏差)，通过标准偏差，我们能知道数据分布的分散程度的最小值。还可以添加 quartiles (四分位数)，以及 Skewness (偏度)，或者其他自己需要的部分。

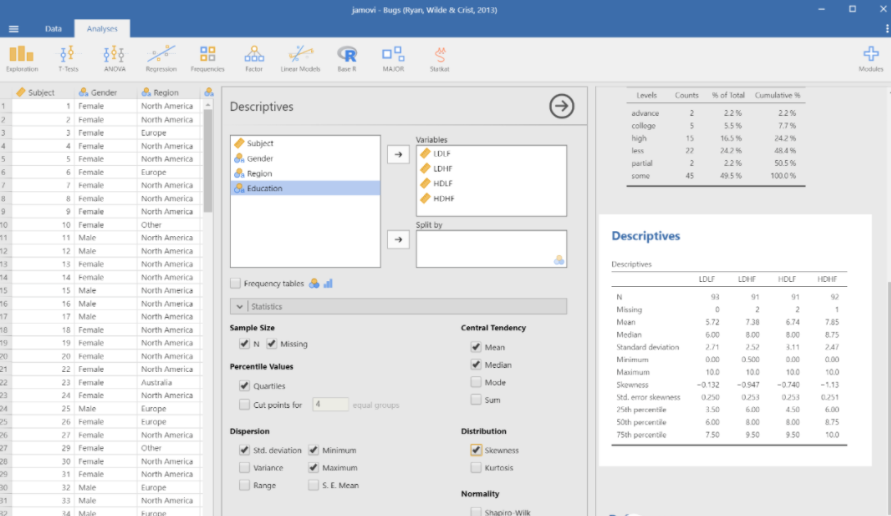
除了上面的对定类变量和定量变量进行基础的数据分析之外，在Jamovi里还有一项值得做的分析就是对定量变量进行分类后再分析。

处理定量变量的一项基本原则是：量最少的一组案例也应该要占到所有案例的10%。因此在上面三个定类变量中，只有性别变量适合用在这里对定量变量进行分类。

这里需要注意的是，因为我们对定量变量进行了分类，数据处理的工作量就增加了，想要很快得到数据的话，可以只简单地选择要分析的项，这里我们只选择了三个，分别是 N，Mean 和 SD。

2. Histograms (直方图)

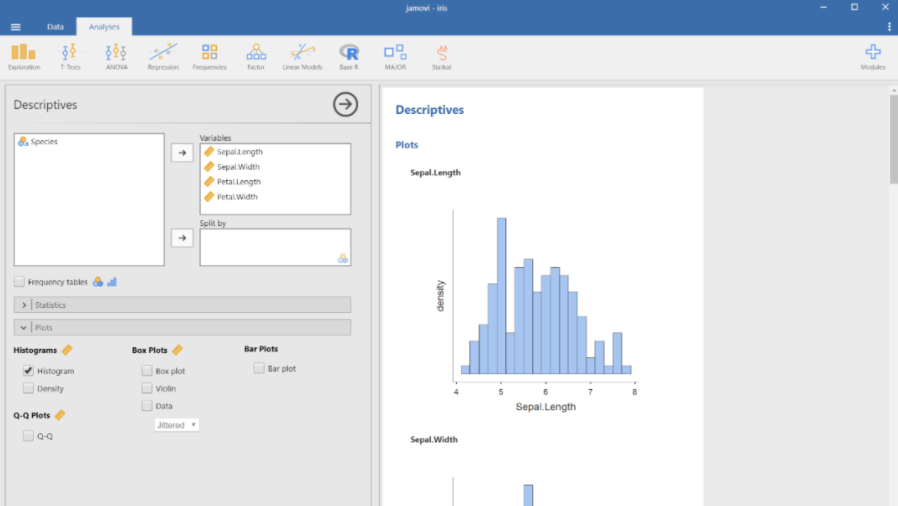
在Jamovi里打开一项数据后，能最直观地看到的是一连串的数字。然而有些时候，比直接看到数字更好的方式其实是先看图表，再将其和具体的数字描述相对应。Jamovi给我们提供了多种图表分析的功能，首先我们来看直方图。

直方图是类似于钟形曲线 (bell curve)的图表，它显示每个分数 (score) 在总体分布中的普遍程度 (钟形曲线/正态曲线：中间高,两端逐渐下降且完全对称)。直方图的每一个条的宽度在Jamovi里是不能修改的，但是颜色可以修改。

在Jamovi里打开 Iris数据。Iris数据研究的是三种虹膜 (鸢尾花) 花瓣和萼片的长度和宽度。

                 （Iris：虹膜/鸢尾花）

选中这四项定量数据。将Statistics下面的默认选项全部取消，点击 Plots下面的直方图，就能得到四个直方图。

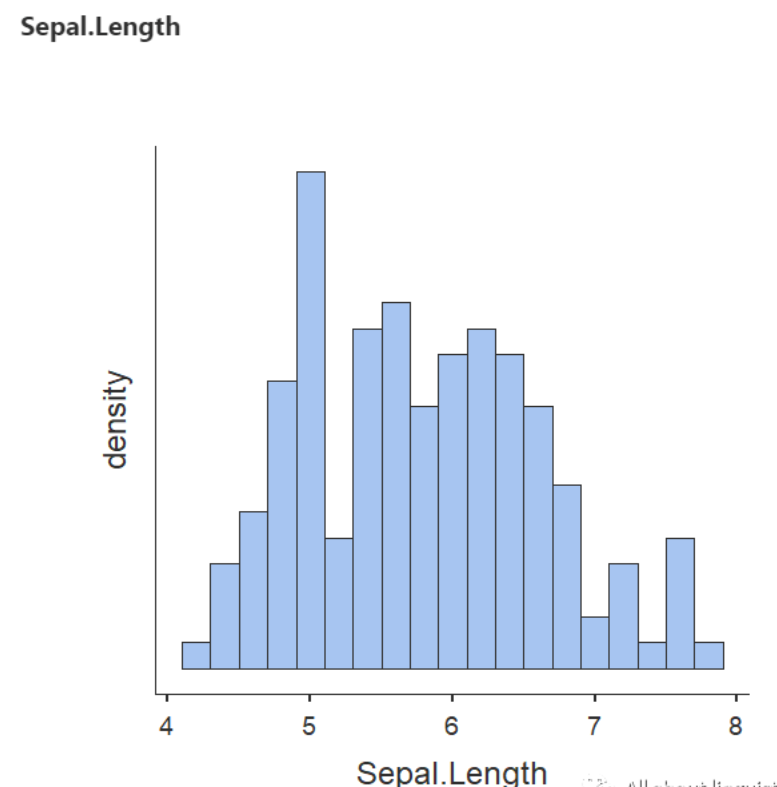
(1) Sepal length 萼片长度

     从下图可以看出，三种鸢尾花的花瓣长度在这里显示出了一个很强的单峰分布 (unimodal distribution)的状态，即，数据分布中只有一个明显峰值。

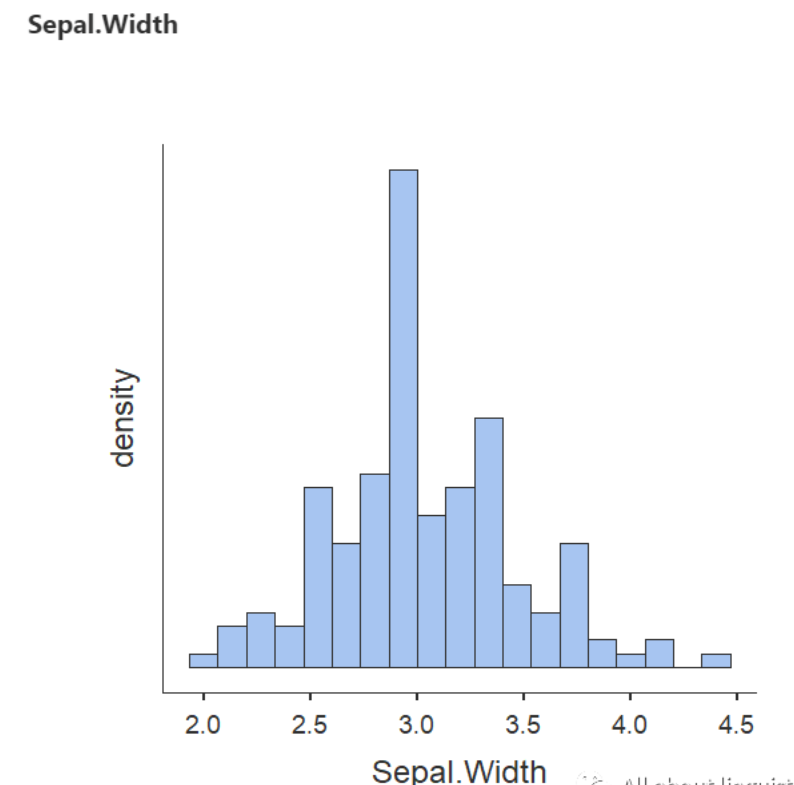
(2) Sepal width 萼片宽度

     萼片宽度整体看起来像是一个正态分布，但在3.0左右的位置有一个很大幅度的增加 (spike)。

(3) Petal length 花瓣长度

     花瓣长度具有很明显的双峰分布 (bimodal distribution)的样子，即，有两个明显的峰值，但也可以看成是两个单独的正态分布。

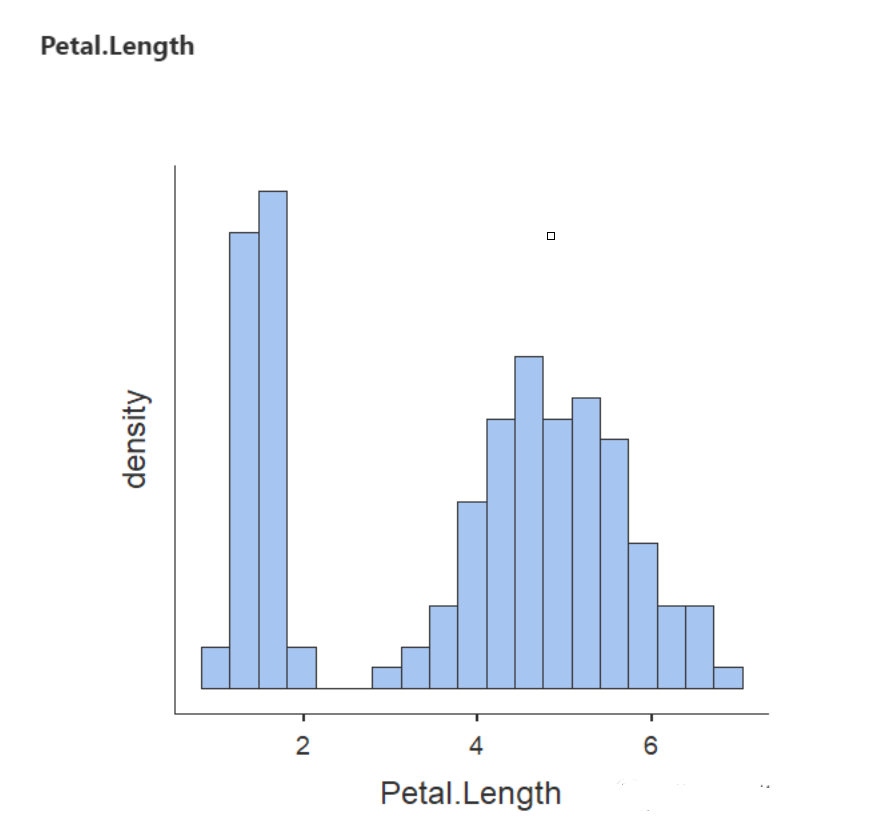
(4) Petal width 花瓣宽度

     花瓣宽度和花瓣长度一样，都显现出了明显的双峰分布 (bimodal distribution)的样子，同时在最左侧出现了偏态分布 (Skewed distribution)，偏态分布中一边的观测值要比另一边的观测值多。

在直方图中，双峰分布通常就意味着有不止一个分布和峰值。在Iris这个数据里，因为它统计了三种不同的鸢尾花的花瓣和萼片的长宽度，出现双峰分布是很正常的。这时，我们可以按照鸢尾花的种类对已有数据再次分类后，再来看每一种鸢尾花的花瓣和萼片的长宽度。

按物种分类后我们会得到各个品种的鸢尾花的堆叠直方图 (stacked histograms)。

三种鸢尾花分别是：

① Setosa     ② Versicolor     ③ Virginica

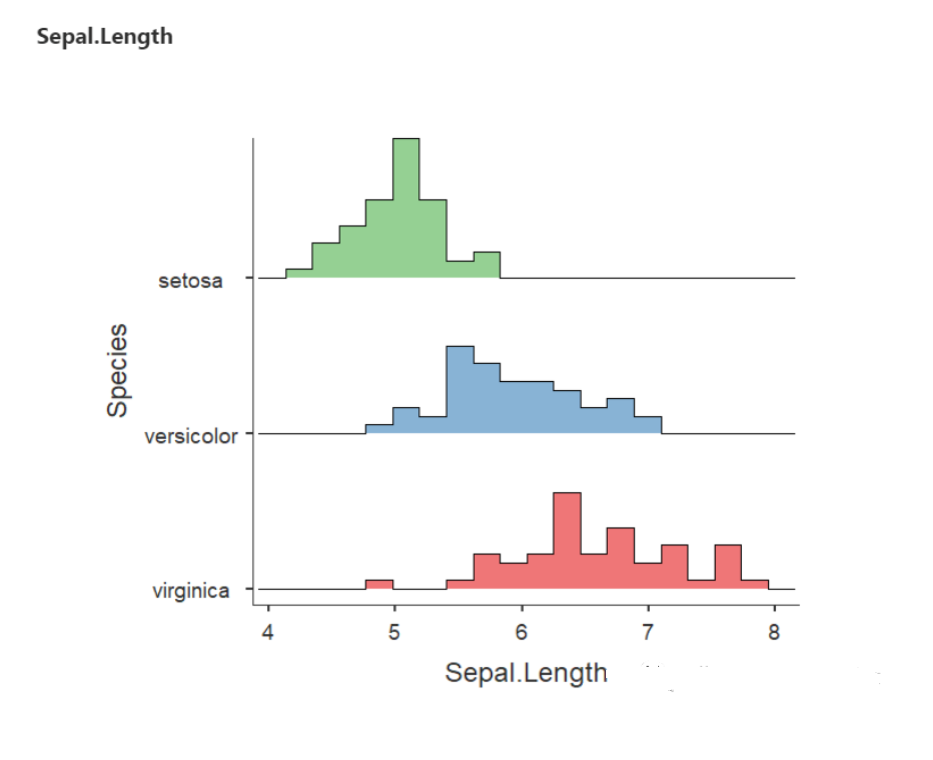
(1) Sepal length 萼片长度

    堆叠直方图的优点是将三个品种的数据全部按相同的比例放置，例如，三种鸢尾花的萼片都在4厘米到8厘米这个范围里。同时三种花用三种不同的颜色来标记了，所以很容易区分。

    从下图里还可以看到，setosa这个品种的萼片长度较短，versicolor这个品种居中，而 virginica这个品种的萼片长度最长。

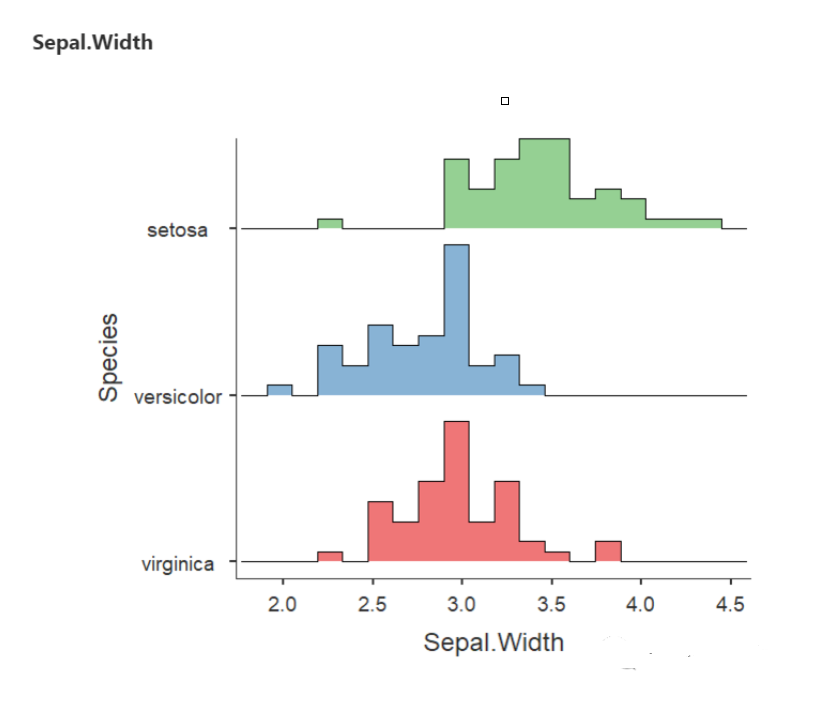
(2) Sepal width 萼片宽度

     就萼片宽度而言，setosa宽度值最高 (尽管setosa有一个异常值)，而 versicolor和 virginica 非常接近。

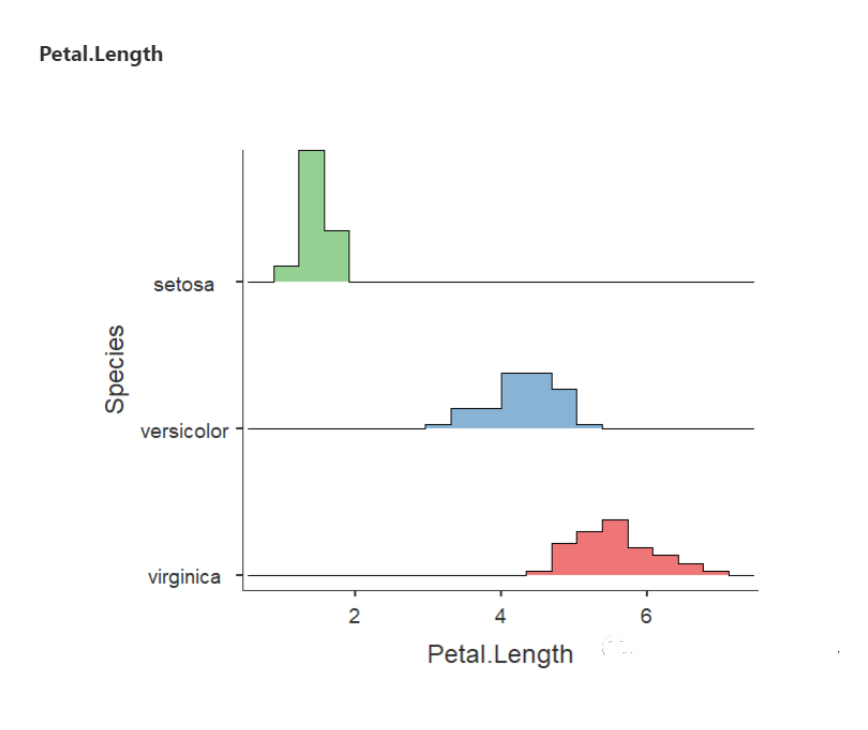
(3) Petal length 花瓣长度

     在花瓣长度上，Setosa和其他两种有很大不同。setosa的花瓣长度几乎都在左侧的最小值附近，而 versicolor 和 virginica 则非常接近。

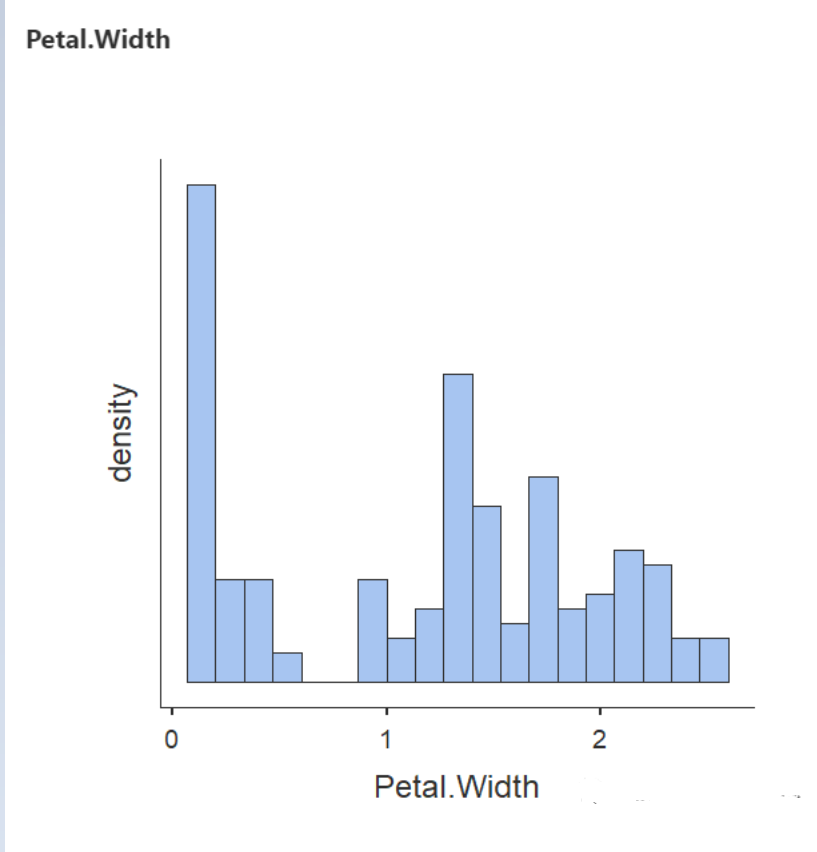
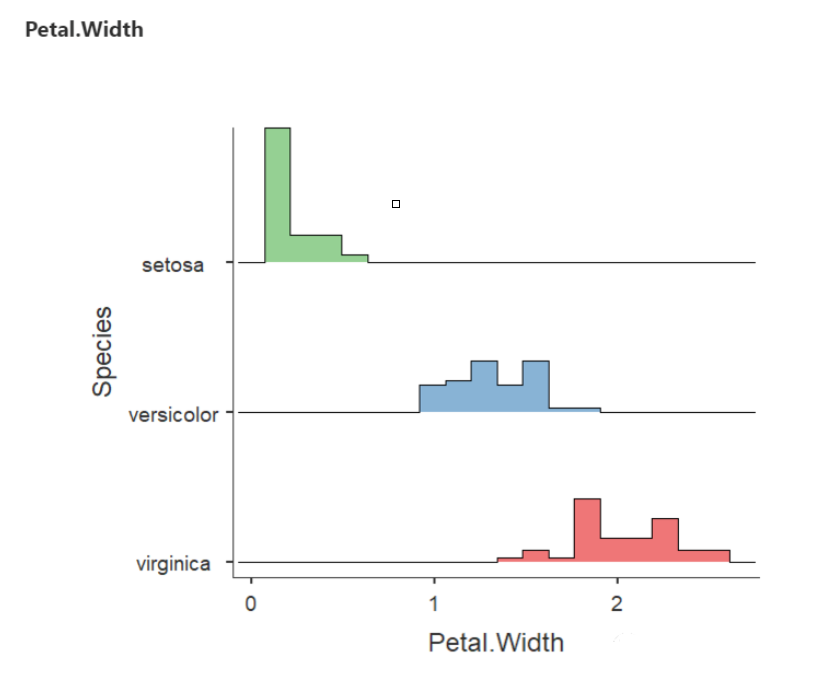
(4) Petal width 花瓣宽度

     最后，在花瓣宽度上，可以看到 satosa有一个实际上接近于零的偏斜分布。而versicolor处于中间位置，virginica具有花瓣宽度的最高值。

总结：

将所有的分组放在一起来比较，进行数据的可视化探索 (visual exploration)是很好的分析数据的方式。看图可以让我们对于某些特殊结果（如双峰分布或偏度）有更多的理解，就像我们刚刚从这些单个的堆叠式小型多重直方图中得到结果一样。在Jamovi中，直方图分析是很好做的，下一次分解数据时试一试吧~

Bugs 数据来源：

https://static.jasp-stats.org/presentations/SARMAC2015/RM/Ryan,%20Wilde,%20Crist,%202013.pdf

Jamovi 03 Exploration 教程资源：

不知道为什么度盘链接出不来，所以先空着。如果有需要的可以发邮件到 1587227525@qq.com，我会用邮箱发给你。

第三部分剩下的内容会在下周更新完。

希望对你有所帮助 :)

欢迎讨论~